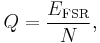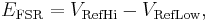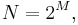Analog-to-digital converter
An analog-to-digital converter (abbreviated ADC, A/D or A to D) is a device that converts a continuous quantity to a discrete time digital representation. An ADC may also provide an isolated measurement. The reverse operation is performed by a digital-to-analog converter (DAC).
Typically, an ADC is an electronic device that converts an input analog voltage or current to a digital number proportional to the magnitude of the voltage or current. However, some non-electronic or only partially electronic devices, such as rotary encoders, can also be considered ADCs.
The digital output may use different coding schemes. Typically the digital output will be a two's complement binary number that is proportional to the input, but there are other possibilities. An encoder, for example, might output a Gray code.
Contents[hide] |
Concepts
Resolution
The resolution of the converter indicates the number of discrete values it can produce over the range of analog values. The values are usually stored electronically in binary form, so the resolution is usually expressed in bits. In consequence, the number of discrete values available, or "levels", is a power of two. For example, an ADC with a resolution of 8 bits can encode an analog input to one in 256 different levels, since 28 = 256. The values can represent the ranges from 0 to 255 (i.e. unsigned integer) or from −128 to 127 (i.e. signed integer), depending on the application.
Resolution can also be defined electrically, and expressed in volts. The minimum change in voltage required to guarantee a change in the output code level is called the least significant bit (LSB) voltage. The resolution Q of the ADC is equal to the LSB voltage. The voltage resolution of an ADC is equal to its overall voltage measurement range divided by the number of discrete voltage intervals:
where N is the number of voltage intervals and EFSR is the full scale voltage range. EFSR is given by
where VRefHi and VRefLow are the upper and lower extremes, respectively, of the voltages that can be coded.
Normally, the number of voltage intervals is given by
where M is the ADC's resolution in bits.
That is, one voltage interval is assigned per code level.
Example:
- Coding scheme as in figure 1 (assume input signal x(t) = Acos(t), A = 5V)
- Full scale measurement range = -5 to 5 volts
- ADC resolution is 8 bits: 28 = 256 quantization levels (codes)
- ADC voltage resolution, Q = (10 V − 0 V) / 256 = 10 V / 256 ≈ 0.039 V ≈ 39 mV.
In practice, the useful resolution of a converter is limited by the best signal-to-noise ratio (SNR) that can be achieved for a digitized signal. An ADC can resolve a signal to only a certain number of bits of resolution, called the effective number of bits (ENOB). One effective bit of resolution changes the signal-to-noise ratio of the digitized signal by 6 dB, if the resolution is limited by the ADC. If a preamplifier has been used prior to A/D conversion, the noise introduced by the amplifier can be an important contributing factor towards the overall SNR.
Response type
Most ADCs are linear types. The term linear implies that the range of input values has a linear relationship with the output value.
Some early converters had a logarithmic response to directly implement A-law or μ-law coding. These encodings are now achieved by using a higher-resolution linear ADC (e.g. 12 or 16 bits) and mapping its output to the 8-bit coded values.
Accuracy
An ADC has several sources of errors. Quantization error and (assuming the ADC is intended to be linear) non-linearity are intrinsic to any analog-to-digital conversion. There is also a so-called aperture error which is due to a clock jitter and is revealed when digitizing a time-variant signal (not a constant value).
These errors are measured in a unit called the least significant bit (LSB). In the above example of an eight-bit ADC, an error of one LSB is 1/256 of the full signal range, or about 0.4%.
Quantization error
Quantization error (or quantization noise) is the difference between the original signal and the digitized signal. Hence, The magnitude of the quantization error at the sampling instant is between zero and half of one LSB. Quantization error is due to the finite resolution of the digital representation of the signal, and is an unavoidable imperfection in all types of ADCs.
Non-linearity
All ADCs suffer from non-linearity errors caused by their physical imperfections, causing their output to deviate from a linear function (or some other function, in the case of a deliberately non-linear ADC) of their input. These errors can sometimes be mitigated by calibration, or prevented by testing.
Important parameters for linearity are integral non-linearity (INL) and differential non-linearity (DNL). These non-linearities reduce the dynamic range of the signals that can be digitized by the ADC, also reducing the effective resolution of the ADC.
Aperture error
Imagine digitizing a sine wave 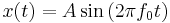 . Provided that the actual sampling time uncertainty due to the clock jitter is
. Provided that the actual sampling time uncertainty due to the clock jitter is 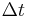 , the error caused by this phenomenon can be estimated as
, the error caused by this phenomenon can be estimated as 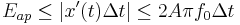 .
.
The error is zero for DC, small at low frequencies, but significant when high frequencies have high amplitudes. This effect can be ignored if it is drowned out by the quantizing error. Jitter requirements can be calculated using the following formula: 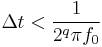 , where q is the number of ADC bits.
, where q is the number of ADC bits.
| Output size (bits) |
Input frequency | ||||||
|---|---|---|---|---|---|---|---|
| 1 Hz | 44.1 kHz | 192 kHz | 1 MHz | 10 MHz | 100 MHz | 1 GHz | |
| 8 | 1,243 µs | 28.2 ns | 6.48 ns | 1.24 ns | 124 ps | 12.4 ps | 1.24 ps |
| 10 | 311 µs | 7.05 ns | 1.62 ns | 311 ps | 31.1 ps | 3.11 ps | 0.31 ps |
| 12 | 77.7 µs | 1.76 ns | 405 ps | 77.7 ps | 7.77 ps | 0.78 ps | 0.08 ps |
| 14 | 19.4 µs | 441 ps | 101 ps | 19.4 ps | 1.94 ps | 0.19 ps | 0.02 ps |
| 16 | 4.86 µs | 110 ps | 25.3 ps | 4.86 ps | 0.49 ps | 0.05 ps | – |
| 18 | 1.21 µs | 27.5 ps | 6.32 ps | 1.21 ps | 0.12 ps | – | – |
| 20 | 304 ns | 6.88 ps | 1.58 ps | 0.16 ps | – | – | – |
| 24 | 19.0 ns | 0.43 ps | 0.10 ps | – | – | – | – |
| 32 | 74.1 ps | – | – | – | – | – | – |
This table shows, for example, that it is not worth using a precise 24-bit ADC for sound recording if there is not an ultra low jitter clock. One should consider taking this phenomenon into account before choosing an ADC.
Clock jitter is caused by phase noise.[1][2] The resolution of ADCs with a digitization bandwidth between 1 MHz and 1 GHz is limited by jitter.[3]
When sampling audio signals at 44.1 kHz, the anti-aliasing filter should have eliminated all frequencies above 22 kHz. The input frequency (in this case, 22 kHz), not the ADC clock frequency, is the determining factor with respect to jitter performance.[4]
Sampling rate
The analog signal is continuous in time and it is necessary to convert this to a flow of digital values. It is therefore required to define the rate at which new digital values are sampled from the analog signal. The rate of new values is called the sampling rate or sampling frequency of the converter.
A continuously varying bandlimited signal can be sampled (that is, the signal values at intervals of time T, the sampling time, are measured and stored) and then the original signal can be exactly reproduced from the discrete-time values by an interpolation formula. The accuracy is limited by quantization error. However, this faithful reproduction is only possible if the sampling rate is higher than twice the highest frequency of the signal. This is essentially what is embodied in the Shannon-Nyquist sampling theorem.
Since a practical ADC cannot make an instantaneous conversion, the input value must necessarily be held constant during the time that the converter performs a conversion (called the conversion time). An input circuit called a sample and hold performs this task—in most cases by using a capacitor to store the analog voltage at the input, and using an electronic switch or gate to disconnect the capacitor from the input. Many ADC integrated circuits include the sample and hold subsystem internally.
Aliasing
All ADCs work by sampling their input at discrete intervals of time. Their output is therefore an incomplete picture of the behaviour of the input. There is no way of knowing, by looking at the output, what the input was doing between one sampling instant and the next. If the input is known to be changing slowly compared to the sampling rate, then it can be assumed that the value of the signal between two sample instants was somewhere between the two sampled values. If, however, the input signal is changing rapidly compared to the sample rate, then this assumption is not valid.
If the digital values produced by the ADC are, at some later stage in the system, converted back to analog values by a digital to analog converter or DAC, it is desirable that the output of the DAC be a faithful representation of the original signal. If the input signal is changing much faster than the sample rate, then this will not be the case, and spurious signals called aliases will be produced at the output of the DAC. The frequency of the aliased signal is the difference between the signal frequency and the sampling rate. For example, a 2 kHz sine wave being sampled at 1.5 kHz would be reconstructed as a 500 Hz sine wave. This problem is called aliasing.
To avoid aliasing, the input to an ADC must be low-pass filtered to remove frequencies above half the sampling rate. This filter is called an anti-aliasing filter, and is essential for a practical ADC system that is applied to analog signals with higher frequency content.
Although aliasing in most systems is unwanted, it should also be noted that it can be exploited to provide simultaneous down-mixing of a band-limited high frequency signal (see undersampling and frequency mixer).
Dither
In A-to-D converters, performance can usually be improved using dither. This is a very small amount of random noise (white noise), which is added to the input before conversion. Its effect is to cause the state of the LSB to randomly oscillate between 0 and 1 in the presence of very low levels of input, rather than sticking at a fixed value. Rather than the signal simply getting cut off altogether at this low level (which is only being quantized to a resolution of 1 bit), it extends the effective range of signals that the A-to-D converter can convert, at the expense of a slight increase in noise - effectively the quantization error is diffused across a series of noise values which is far less objectionable than a hard cutoff. The result is an accurate representation of the signal over time. A suitable filter at the output of the system can thus recover this small signal variation.
An audio signal of very low level (with respect to the bit depth of the ADC) sampled without dither sounds extremely distorted and unpleasant. Without dither the low level may cause the least significant bit to "stick" at 0 or 1. With dithering, the true level of the audio may be calculated by averaging the actual quantized sample with a series of other samples [the dither] that are recorded over time.
A virtually identical process, also called dither or dithering, is often used when quantizing photographic images to a fewer number of bits per pixel—the image becomes noisier but to the eye looks far more realistic than the quantized image, which otherwise becomes banded. This analogous process may help to visualize the effect of dither on an analogue audio signal that is converted to digital.
Dithering is also used in integrating systems such as electricity meters. Since the values are added together, the dithering produces results that are more exact than the LSB of the analog-to-digital converter.
Note that dither can only increase the resolution of a sampler, it cannot improve the linearity, and thus accuracy does not necessarily improve.
Oversampling
Usually, signals are sampled at the minimum rate required, for economy, with the result that the quantization noise introduced is white noise spread over the whole pass band of the converter. If a signal is sampled at a rate much higher than the Nyquist frequency and then digitally filtered to limit it to the signal bandwidth there are the following advantages:
- digital filters can have better properties (sharper rolloff, phase) than analogue filters, so a sharper anti-aliasing filter can be realised and then the signal can be downsampled giving a better result
- a 20-bit ADC can be made to act as a 24-bit ADC with 256× oversampling
- the signal-to-noise ratio due to quantization noise will be higher than if the whole available band had been used. With this technique, it is possible to obtain an effective resolution larger than that provided by the converter alone
- The improvement in SNR is 3 dB (equivalent to 0.5 bits) per octave of oversampling which is not sufficient for many applications. Therefore, oversampling is usually coupled with noise shaping (see sigma-delta modulators). With noise shaping, the improvement is 6L+3 dB per octave where L is the order of loop filter used for noise shaping. e.g. - a 2nd order loop filter will provide an improvement of 15 dB/octave.
Relative speed and precision
The speed of an ADC varies by type. The Wilkinson ADC is limited by the clock rate which is processable by current digital circuits. Currently, frequencies up to 300 MHz are possible. The conversion time is directly proportional to the number of channels. For a successive-approximation ADC, the conversion time scales with the logarithm of the number of channels. Thus for a large number of channels, it is possible that the successive-approximation ADC is faster than the Wilkinson. However, the time consuming steps in the Wilkinson are digital, while those in the successive-approximation are analog. Since analog is inherently slower than digital, as the number of channels increases, the time required also increases. Thus there are competing processes at work. Flash ADCs are certainly the fastest type of the three. The conversion is basically performed in a single parallel step. For an 8-bit unit, conversion takes place in a few tens of nanoseconds.
There is, as expected, somewhat of a tradeoff between speed and precision. Flash ADCs have drifts and uncertainties associated with the comparator levels, which lead to poor uniformity in channel width. Flash ADCs have a resulting poor linearity. For successive-approximation ADCs, poor linearity is also apparent, but less so than for flash ADCs. Here, non-linearity arises from accumulating errors from the subtraction processes. Wilkinson ADCs are the best of the three. These have the best differential non-linearity. The other types require channel smoothing in order to achieve the level of the Wilkinson.[5][6]
The sliding scale principle
The sliding scale or randomizing method can be employed to greatly improve the channel width uniformity and differential linearity of any type of ADC, but especially flash and successive approximation ADCs. Under normal conditions, a pulse of a particular amplitude is always converted to a certain channel number. The problem lies in that channels are not always of uniform width, and the differential linearity decreases proportionally with the divergence from the average width. The sliding scale principle uses an averaging effect to overcome this phenomenon. A random, but known analog voltage is added to the input pulse. It is then converted to digital form, and the equivalent digital version is subtracted, thus restoring it to its original value. The advantage is that the conversion has taken place at a random point. The statistical distribution of the final channel numbers is decided by a weighted average over a region of the range of the ADC. This in turn desensitizes it to the width of any given channel.[7][8]
ADC types
These are the most common ways of implementing an electronic ADC:
- A direct-conversion ADC or flash ADC has a bank of comparators sampling the input signal in parallel, each firing for their decoded voltage range. The comparator bank feeds a logic circuit that generates a code for each voltage range. Direct conversion is very fast, capable of gigahertz sampling rates, but usually has only 8 bits of resolution or fewer, since the number of comparators needed, 2N - 1, doubles with each additional bit, requiring a large, expensive circuit. ADCs of this type have a large die size, a high input capacitance, high power dissipation, and are prone to produce glitches at the output (by outputting an out-of-sequence code). Scaling to newer submicrometre technologies does not help as the device mismatch is the dominant design limitation. They are often used for video, wideband communications or other fast signals in optical storage.
- A successive-approximation ADC uses a comparator to successively narrow a range that contains the input voltage. At each successive step, the converter compares the input voltage to the output of an internal digital to analog converter which might represent the midpoint of a selected voltage range. At each step in this process, the approximation is stored in a successive approximation register (SAR). For example, consider an input voltage of 6.3 V and the initial range is 0 to 16 V. For the first step, the input 6.3 V is compared to 8 V (the midpoint of the 0–16 V range). The comparator reports that the input voltage is less than 8 V, so the SAR is updated to narrow the range to 0–8 V. For the second step, the input voltage is compared to 4 V (midpoint of 0–8). The comparator reports the input voltage is above 4 V, so the SAR is updated to reflect the input voltage is in the range 4–8 V. For the third step, the input voltage is compared with 6 V (halfway between 4 V and 8 V); the comparator reports the input voltage is greater than 6 volts, and search range becomes 6–8 V. The steps are continued until the desired resolution is reached.
- A ramp-compare ADC produces a saw-tooth signal that ramps up or down then quickly returns to zero. When the ramp starts, a timer starts counting. When the ramp voltage matches the input, a comparator fires, and the timer's value is recorded. Timed ramp converters require the least number of transistors. The ramp time is sensitive to temperature because the circuit generating the ramp is often just some simple oscillator. There are two solutions: use a clocked counter driving a DAC and then use the comparator to preserve the counter's value, or calibrate the timed ramp. A special advantage of the ramp-compare system is that comparing a second signal just requires another comparator, and another register to store the voltage value. A very simple (non-linear) ramp-converter can be implemented with a microcontroller and one resistor and capacitor.[9] Vice versa, a filled capacitor can be taken from an integrator, time-to-amplitude converter, phase detector, sample and hold circuit, or peak and hold circuit and discharged. This has the advantage that a slow comparator cannot be disturbed by fast input changes.
- The Wilkinson ADC was designed by D. H. Wilkinson in 1950. The Wilkinson ADC is based on the comparison of an input voltage with that produced by a charging capacitor. The capacitor is allowed to charge until its voltage is equal to the amplitude of the input pulse (a comparator determines when this condition has been reached). Then, the capacitor is allowed to discharge linearly, which produces a ramp voltage. At the point when the capacitor begins to discharge, a gate pulse is initiated. The gate pulse remains on until the capacitor is completely discharged. Thus the duration of the gate pulse is directly proportional to the amplitude of the input pulse. This gate pulse operates a linear gate which receives pulses from a high-frequency oscillator clock. While the gate is open, a discrete number of clock pulses pass through the linear gate and are counted by the address register. The time the linear gate is open is proportional to the amplitude of the input pulse, thus the number of clock pulses recorded in the address register is proportional also. Alternatively, the charging of the capacitor could be monitored, rather than the discharge.[10][11]
- An integrating ADC (also dual-slope or multi-slope ADC) applies the unknown input voltage to the input of an integrator and allows the voltage to ramp for a fixed time period (the run-up period). Then a known reference voltage of opposite polarity is applied to the integrator and is allowed to ramp until the integrator output returns to zero (the run-down period). The input voltage is computed as a function of the reference voltage, the constant run-up time period, and the measured run-down time period. The run-down time measurement is usually made in units of the converter's clock, so longer integration times allow for higher resolutions. Likewise, the speed of the converter can be improved by sacrificing resolution. Converters of this type (or variations on the concept) are used in most digital voltmeters for their linearity and flexibility.
- A delta-encoded ADC or counter-ramp has an up-down counter that feeds a digital to analog converter (DAC). The input signal and the DAC both go to a comparator. The comparator controls the counter. The circuit uses negative feedback from the comparator to adjust the counter until the DAC's output is close enough to the input signal. The number is read from the counter. Delta converters have very wide ranges and high resolution, but the conversion time is dependent on the input signal level, though it will always have a guaranteed worst-case. Delta converters are often very good choices to read real-world signals. Most signals from physical systems do not change abruptly. Some converters combine the delta and successive approximation approaches; this works especially well when high frequencies are known to be small in magnitude.
- A pipeline ADC (also called subranging quantizer) uses two or more steps of subranging. First, a coarse conversion is done. In a second step, the difference to the input signal is determined with a digital to analog converter (DAC). This difference is then converted finer, and the results are combined in a last step. This can be considered a refinement of the successive-approximation ADC wherein the feedback reference signal consists of the interim conversion of a whole range of bits (for example, four bits) rather than just the next-most-significant bit. By combining the merits of the successive approximation and flash ADCs this type is fast, has a high resolution, and only requires a small die size.
- A sigma-delta ADC (also known as a delta-sigma ADC) oversamples the desired signal by a large factor and filters the desired signal band. Generally, a smaller number of bits than required are converted using a Flash ADC after the filter. The resulting signal, along with the error generated by the discrete levels of the Flash, is fed back and subtracted from the input to the filter. This negative feedback has the effect of noise shaping the error due to the Flash so that it does not appear in the desired signal frequencies. A digital filter (decimation filter) follows the ADC which reduces the sampling rate, filters off unwanted noise signal and increases the resolution of the output (sigma-delta modulation, also called delta-sigma modulation).
- A time-interleaved ADC uses M parallel ADCs where each ADC sample data every M:th cycle of the effective sample clock. The result is that the sample rate is increased M times compared to what each individual ADC can manage. In practice, the individual differences between the M ADCs degrade the overall performance reducing the SFDR. However, technologies exist to correct for these time-interleaving mismatch errors.
- An ADC with intermediate FM stage first uses a voltage-to-frequency converter to convert the desired signal into an oscillating signal with a frequency proportional to the voltage of the desired signal, and then uses a frequency counter to convert that frequency into a digital count proportional to the desired signal voltage. Longer integration times allow for higher resolutions. Likewise, the speed of the converter can be improved by sacrificing resolution. The two parts of the ADC may be widely separated, with the frequency signal passed through an opto-isolator or transmitted wirelessly. Some such ADCs use sine wave or square wave frequency modulation; others use pulse-frequency modulation. Such ADCs were once the most popular way to show a digital display of the status of a remote analog sensor.[12][13][14][15][16]
There can be other ADCs that use a combination of electronics and other technologies:
- A time-stretch analog-to-digital converter (TS-ADC) digitizes a very wide bandwidth analog signal, that cannot be digitized by a conventional electronic ADC, by time-stretching the signal prior to digitization. It commonly uses a photonic preprocessor frontend to time-stretch the signal, which effectively slows the signal down in time and compresses its bandwidth. As a result, an electronic backend ADC, that would have been too slow to capture the original signal, can now capture this slowed down signal. For continuous capture of the signal, the frontend also divides the signal into multiple segments in addition to time-stretching. Each segment is individually digitized by a separate electronic ADC. Finally, a digital signal processor rearranges the samples and removes any distortions added by the frontend to yield the binary data that is the digital representation of the original analog signal.
Commercial analog-to-digital converters
These are usually integrated circuits.
Most converters sample with 6 to 24 bits of resolution, and produce fewer than 1 megasample per second. Thermal noise generated by passive components such as resistors masks the measurement when higher resolution is desired. For audio applications and in room temperatures, such noise is usually a little less than 1 μV (microvolt) of white noise. If the MSB corresponds to a standard 2 V of output signal, this translates to a noise-limited performance that is less than 20~21 bits, and obviates the need for any dithering. As of February 2002, Mega- and giga-sample per second converters are available. Mega-sample converters are required in digital video cameras, video capture cards, and TV tuner cards to convert full-speed analog video to digital video files. Commercial converters usually have ±0.5 to ±1.5 LSB error in their output.
In many cases, the most expensive part of an integrated circuit is the pins, because they make the package larger, and each pin has to be connected to the integrated circuit's silicon. To save pins, it is common for slow ADCs to send their data one bit at a time over a serial interface to the computer, with the next bit coming out when a clock signal changes state, say from 0 to 5 V. This saves quite a few pins on the ADC package, and in many cases, does not make the overall design any more complex (even microprocessors which use memory-mapped I/O only need a few bits of a port to implement a serial bus to an ADC).
Commercial ADCs often have several inputs that feed the same converter, usually through an analog multiplexer. Different models of ADC may include sample and hold circuits, instrumentation amplifiers or differential inputs, where the quantity measured is the difference between two voltages.
Applications
Music recording
ADCs are integral to current music reproduction technology. Since much music production is done on computers, when an analog recording is used, an ADC is needed to create the PCM data stream that goes onto a compact disc or digital music file.
The current crop of AD converters utilized in music can sample at rates up to 192 kilohertz. High bandwidth headroom allows the use of cheaper or faster anti-aliasing filters of less severe filtering slopes. The proponents of oversampling assert that such shallower anti-aliasing filters produce less deleterious effects on sound quality, exactly because of their gentler slopes. Others prefer entirely filterless AD conversion, arguing that aliasing is less detrimental to sound perception than pre-conversion brickwall filtering. Considerable literature exists on these matters, but commercial considerations often play a significant role. Most high-profile recording studios record in 24-bit/192-176.4 kHz PCM or in DSD formats, and then downsample or decimate the signal for Red-Book CD production (44.1 kHz) or to 48 kHz for commonly used for radio/TV broadcast applications.
Digital signal processing
AD converters are used virtually everywhere where an analog signal has to be processed, stored, or transported in digital form. Fast video ADCs are used, for example, in TV tuner cards. Slow on-chip 8, 10, 12, or 16 bit ADCs are common in microcontrollers. Very fast ADCs are needed in Digital storage oscilloscopes, and are crucial for new applications like software defined radio.
Electrical Symbol
Testing
Testing an Analog to Digital Converter requires an analog input source, hardware to send control signals and capture digital data output. Some ADCs also require an accurate source of reference signal.
The key parameters to test a SAR ADC are following:
- DC Offset Error
- DC Gain Error
- Signal to Noise ration (SNR)
- Total Harmonic Distortion (THD)
- Integral Non Linearity (INL)
- Differential Non Linearity (DNL)
- Spurious Free Dynamic Range
- Power Dissipation
See also
- Audio converter
- Beta encoder
- Digital signal processing
- Quantization (signal processing)
- Modem
- Differential linearity
- Sample-and-hold amplifier
- Ideal sampler
- Integral linearity
Notes
- ^ Maxim App 800: "Design a Low-Jitter Clock for High-Speed Data Converters"
- ^ "Jitter effects on Analog to Digital and Digital to Analog Converters"
- ^ abstract: "The effects of aperture jitter and clock jitter in wideband ADCs" by Michael Löhning and Gerhard Fettweis 2007
- ^ "Understanding the effect of clock jitter on high-speed ADCs" by Derek Redmayne & Alison Steer 2008
- ^ Knoll (1989, p. 664–665)
- ^ Nicholson (1974, p. 313–315)
- ^ Knoll (1989, p. 665–666)
- ^ Nicholson (1974, p. 315–316)
- ^ Atmel Application Note AVR400: Low Cost A/D Converter
- ^ Knoll (1989, p. 663–664)
- ^ Nicholson (1974, p. 309–310)
- ^ [www.analog.com/static/imported-files/tutorials/MT-028.pdf Analog Devices MT-028 Tutorial: "Voltage-to-Frequency Converters"] by Walt Kester and James Bryant 2009, apparently adapted from "Data conversion handbook" by Walter Allan Kester 2005, page 274
- ^ [ww1.microchip.com/downloads/en/AppNotes/00795a.pdf Microchip AN795 "Voltage to Frequency / Frequency to Voltage Converter"] page 4: "13-bit A/D converter"
- ^ "Elements of electronic instrumentation and measurement" by Joseph J. Carr 1996, page 402
- ^ "Voltage-to-Frequency Analog-to-Digital Converters"
- ^ "Troubleshooting Analog Circuits" by Robert A. Pease 1991, p. 130
References
- Allen, Phillip E.; Holberg, Douglas R., CMOS Analog Circuit Design, ISBN 0-19-511644-5
- Kester, Walt, ed. (2005), The Data Conversion Handbook, Elsevier: Newnes, ISBN 0-7506-7841-0, http://www.analog.com/library/analogDialogue/archives/39-06/data_conversion_handbook.html
- Johns, David; Martin, Ken, Analog Integrated Circuit Design, ISBN 0-471-14448-7
- Knoll, Glenn F. (1989), Radiation Detection and Measurement (2nd ed.), New York: John Wiley & Sons, pp. 665–666
- Liu, Mingliang, Demystifying Switched-Capacitor Circuits, ISBN 0-7506-7907-7
- Nicholson, P. W. (1974), Nuclear Electronics, New York: John Wiley & Sons, pp. 315–316
- Norsworthy, Steven R.; Schreier, Richard; Temes, Gabor C. (1997), Delta-Sigma Data Converters, IEEE Press, ISBN 0-7803-1045-4
- Razavi, Behzad (1995), Principles of Data Conversion System Design, New York, NY: IEEE Press, ISBN 0-7803-1093-4
- Staller, Len (February 24, 2005), "Understanding analog to digital converter specifications", Embedded Systems Design, http://www.embedded.com/showArticle.jhtml?articleID=60403334
- Walden, R. H. (1999), "Analog-to-digital converter survey and analysis", IEEE Journal on Selected Areas in Communications 17 (4): 539–550, doi:10.1109/49.761034, ISSN 0733-8716, http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=761034
External links
- Counting Type ADC A simple tutorial showing how to build your first ADC.
- An Introduction to Delta Sigma Converters A very nice overview of Delta-Sigma converter theory.
- Digital Dynamic Analysis of A/D Conversion Systems through Evaluation Software based on FFT/DFT Analysis RF Expo East, 1987
- Which ADC Architecture Is Right for Your Application? article by Walt Kester
- AN71 - The Care and Feeding of High Performance ADCs Real world circuit and layout advice
- ADC and DAC Glossary Defines commonly used technical terms.
- Signal processing and system aspects of time-interleaved ADCs.
- Introduction to ADC in AVR - Analog to digital conversion with Atmel microcontrollers